關鍵詞：課堂教學開放型探索材料訓練題
　　摘要：在課堂教學中，提倡教育創新，積極開發和培養學生的創新能力。課堂教學必須突出“以人的發展為本”，也就是在教學的全過程中使學生積極主動的參與學習。“開放型”教學恰恰符合了這一教學改革的要求，它的課堂教學主要形式就是要求學生參與多向思維，通過不同角度的探索，自己去獲取、鞏固和深化知識，并在參與的全過程中發展思維，培養能力。
　　一、 創設“開放型”的課堂教學環境
　　課堂教學環境是課堂內各種因素的集合。“它是由課堂空間，課堂師生人際關系，課堂生活質量和課堂社會氣氛因素構成的課堂生活情境”。“開放型”的課堂教學環境的研究，也主要是如何創設一種開放型的課堂教學空間，開放型的課堂師生關系和開放型的課堂教學氣氛。
　　在課堂教學空間方面，為了有利于學生多向交流，促進參與，我們在學生座位編排上，不局限于兩人一桌，全體學生面向講臺的單一坐法。經常根據教學內容，可采用四人或多人圍坐，甚至坐成半圓弧形式，便于展開小組協作交流，打破拘束呆板的學習空間。
　　在課堂師生人際關系上，應創設一種和諧、寬松的教學環境。使學生感到教師是自己的親密朋友，平等相待，和藹可親，老師與學生、學生與學生相互之間交流民主，達到較為開放的教學氛圍。所以要求老師在教學中把學生當成學習的主人，用商量的口氣與學生展開討論。如我們在教學“按比例分配應用題”時，先向學生提出下列問題：“植樹節如果學校要我們七年級（1）班和七年級（2）班同學種360棵樹苗，你們想一想按怎樣的比例分配，兩班各應多少棵？”這時許多同學先想到的是平均分，老師提出平均分就是兩班所種棵數的比是幾比幾？學生答：“按1：1分配”。接著又有許多同學提出：按兩班人數的比來分配，也有提出按2：1、5：4、3：2......來分配。一下子說出不同的比，而大部分同學都考慮自己的班多種些。在這種情況的創設之下，學生對“比”的認識又一次得到深化，同時在說“比”的過程中又反映了學生的不同思想。接著教師說：“那好吧！既然同學們有不同的分配方法，計算出我們兩個班所種的棵數。”可見，這種教法教師非常巧妙地創設了開放性的引入情境，充分調動了學生學習的積極性和主動性，學生能從自己的不同想法中自覺地進入了新知的探索。
　　二、提供“開放型”的探索材料
　　“開放型”材料的提供，首先要遵循的一條原則是：能使學生投入多向思維，達到問題解決。也就是說教師給學生的學習材料既要使學生感興趣，能激起學生學習的積極性，又要做到材料與內容相吻合，還要使學生展開積極思維，同時在多向參與的過程中，尋求規律，掌握知識。提供“開放型”的探索材料，我認為首先要做到以下兩點：
　　（1）要使學生在選擇材料上有一定的自由。
　　如在教學“平行線的判定”一課中，我們給提供了以下材料：“兩條直線被第三條直線所截同位角相等、內錯角相等，同旁內角互補能判斷兩條直線什么樣的位置關系？這樣學生在實踐活動中自由度大，他們不知不覺地發揮了平常的生活經驗去解決問題。經過一段時間探索，教師根據學生不同的想法把典型的圖形學生畫在黑板上，再接著引發學生觀察矯正，從中掌握平行線的判斷方法。在這種開放性的自主探索平行線的判斷方法中，學生感到學習是自己的事，以積極主動的態度參與思考。
　　（2）要使學生問題在思考過程中有一定的開放度。
　　如在教學“比多（少）求和”兩步計算應用題，教材里有這樣一個例題：“果園里有蘋果樹1420棵，梨樹比蘋果樹少280棵。蘋果樹和梨樹共有多少棵？”我們在教學此例時沒有直接單一的引入例題，而是讓學生自己來編出多個，以最后“求和”為基本數量關系的應用題。教學過程如下：
　　第一步給出一個問題：“蘋果樹和梨樹一共多少棵？”問學生：“你們看到這個問題想到了什么？”讓學生補上蘋果樹和梨樹各有多少棵，教師對具體數據略加調整寫出：“果園有蘋果樹1400棵，梨樹1100棵，蘋果樹和梨樹一共有多少棵？”
　　第二步要求學生改編其中一個條件，使它成為兩步計算應用題，分組討論到底有幾種改編方法，并分別列出算式解答。
　　第三步教師提出：以上這四種改編方法為什么只有兩種列式方法？這兩種解題過程的相同點和不同點在什么地方？再次組織學生分組討論，進一步認識題目的結構和解題方法。
　　由此看來，以上的教法改變了傳統的例題教學，采用開放性的編題引入。使學生在主動構建的過程中，認識這類兩步計算應用題的橫向聯系，從整體上把握了解題規律,同時在這一過程中訓練了思維能力，使學生體驗到獲取新知的成功感。
　　三、設計“開放型”的訓練題
　　經過研究和總結，我們把“開放型”習題分成以下六種類型。
　　1．答案不唯一。
　　也就是一題有多種答案，甚至有無數多個解答結果，而且大部分的題在解出不同結果的同時能總結出解題規律。如一位教師在教學“三角形面積計算”之后，設計了如下的深化題：“在下圖平行四邊形中畫上一條直線，把平行四邊形分成兩個面積完全相等的圖形。”
　　
　　
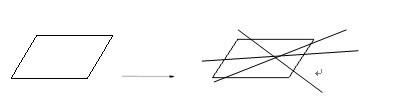
　　一般學生先想到的是畫對角線把平行四邊形分成兩個相等的三角形。當然，這種畫法對本課三角形面積計算方法的推導又一次得到認識。接著引導學生繼續思考，學生會很快地發現只要通過平行四邊形對角線交點的直線都能把平行四邊形分成兩個面積相等的圖形，而且有無數多對相等的梯形。通過此題開放性的操作、觀察、思考，為后繼學習梯形面積計算作好了孕伏。
　　2．條件不唯一
　　學生通過對題目先從不同角度補上條件，然后解答。這種訓練在應用題教學中較為常見，如下題要求學生補上一個條件使它成為三步計算應用題：“某農機廠今年四月份生產插秧機240臺，————，四、五月份共生產多少臺？”此題條件的補充方法很多，學生可根據自己的能力補充不同條件，解答出結果。
　　3．問題不唯一
　　也就是使學生在補充不同問題中，得出不同解答。如：“一個運輸隊運送糧食，上午運走300袋，每袋50千克；下午運走1800千克，每袋是50千克。”學生可以補上如下問題：這一天共運走了多少千克？下午比上午多運多少克？下午運送的重量是上午的多少倍？下午比上午多運多少袋？
　　4．解法不唯一
　　教學中設計一題多解的訓練，應是開放型訓練的一種類型。如：“一輛汽車從甲地開往乙地，3。5小時剛好行使了全程的3/5，照這樣速度，行完全程還要幾小時？”學生在解答時，展開不同思路，得出四種解法。
　　5．解題不唯一
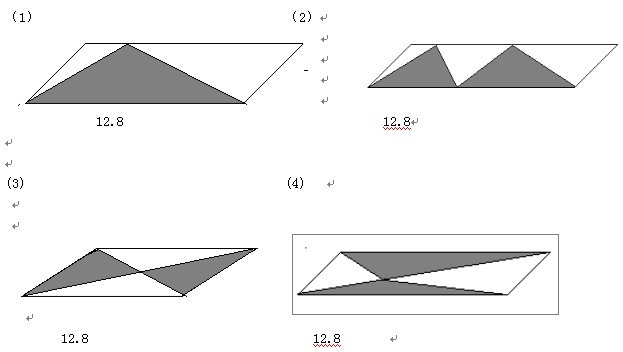
　　所謂解題不唯一，是指學生根據自己的能力或興趣，選擇自己喜歡的題目。改變以往教師給學生在數量和對象上都是劃一的做法。如在教學“三角形面積計算”后，提供以下一組題目，讓學生根據自己的能力選擇一題進行計算。（1）----（4）題都是求陰影部分面積。底邊長都是12.8厘米，高都是8厘米。
　　
　　　　

　　
　　
　　除按題的難易層次，放開讓學生選擇之外，有時還可以引發學生根據自己的能力，在練習的題量上有所不同。
　　6．解題策略不唯一
　　所謂解題策略不唯一，就是解答問題的方案有多種可以使學生更好得到思維訓練。在解答這一實際問題過程中，學生采取的策略顯然不唯一。這樣既熟練了此類問題的數量關系，又提高了學生解決實際問題的能力。
　　總之，“開放性”的教學能更好地發揮學生學習的主動性，為全方位參與創造了條件，能更好地滿足每個學生學習的心理需要，使學生的良好的個性品質得到充分發展，能更好地啟迪思維，使學生的創新意識和能力得到較好的培養。讓我們從每一節課做起，真正地把學生看成是“發展中的人”，在充滿生命活力與和諧氣氛的教學環境中，師生共同參與、相互作用、摩擦出智慧的火花，結出創造之果。