摘要：本文以MATLAB神經網絡工具箱為平臺，建立了BP-LM和LVQ兩種地表水神經網絡水質評價模型。研究結果表明，BP-LM網絡的計算速度和收斂速度遠高于LVQ網絡，BP-LM網絡模型比較適合于水質評價。本文也觀察了大小樣本對網絡模型訓練的影響，發現LVQ網絡模型不適宜用大訓練樣本進行訓練，而BP-LM網絡對訓練樣本的大小不敏感，這有助于構建大容量有代表性的訓練樣本。
　　關鍵詞：人工神經網絡；BP-LM網絡；LVQ網絡；訓練樣本；水質評價
　　
　　1前言
　　水是人類生存和發展的物質基礎。隨著生產的發展和人口的增長，水資源短缺、水質污染問題越來越突出。水環境質量評價是認識和研究水環境的一項重要內容，其目的是準確反映環境的質量和污染狀況，預測未來的發展趨勢，是水環境管理保護和治理的一項重要基礎性工作。水環境質量評價是指通過對水體的一些物理、化學、生物指標的監測、調查，根據不同的目的和要求，按一定的方法對水體的質量做出估計。通過對水質進行評價，確定其污染類型，準確地指出水體當時的污染程度，為保護水體、水質提供方向性、原則性的方案和依據。
　　由于影響水質的因素很多，且因素與水質類別之間通常存在復雜的非線性關系，所以迄今沒有一種統一的和公認的評價方法。目前應用于水質評價的方法發展了很多，大多是基于傳統數學（統計學）、模糊數學和灰色數學的評價模型，如單項污染指數法、綜合污染指數法、模糊綜合評判法、灰色關聯度分析法、灰色局勢決策法、物元分析法等[1-2]。單項污染指數法只能評價水體中某種污染物的危害程度，不能反映水體中各種污染物的綜合影響；綜合污染指數法采用一個簡單的數字指標作為硬性界限，忽視了這種分類或分級界限的模糊性；而基于模糊數學和灰色數學的綜合評價方法，雖然注意到了這種實際上存在的分類或分級的模糊性，但在各水質污染物指標權重的選擇上常帶有主觀性和隨意性，因而存在一定的局限性。
　　人工神經網絡（ArtificialNeuralNetwork，簡稱ANN）是起源于20世紀40年代，在80年代取得突破并迅速發展和廣泛應用于眾多學科的非線性模擬技術，是目前最活躍的前沿科學之一。ANN是對人腦神經元巨系統的生理特征和功能的抽象和模擬，具有自適應、自學習的特點，非常適合于研究和解決復雜的非線性問題。
　　從80年代末開始，我國的環境保護工作者開始將神經網絡技術引入環境質量評價工作，建立了基于誤差反向傳播（BP）網絡、霍普菲爾德（Hopfield）網絡、徑向基函數（RBF）網絡、自組織特征映射（SOFM）網絡、學習向量量化（LVQ）網絡等數10多種評價模型，但其中80-90%是基于BP網絡模型及其變化模型[2]。
　　本研究針對地表水環境質量評價，以MathWorks公司開發的MATLAB（R14SP1）神經網絡工具箱（4.0.4版本）為平臺，建立了基于Levenberg-Marquardt訓練算法的BP網絡的評價模型（BP-LM）和基于LVQ網絡的評價模型（LVQ），分別用大訓練樣本和小訓練樣本進行訓練，用檢測樣本評價訓練效果及網絡模型的性能，比較分析大、小訓練樣本對網絡模型訓練的影響以及兩種模型的優劣。
　　2訓練樣本的準備
　　在神經網絡模型的建立之中，訓練樣本占有非常重要的位置。在進行模式識別的過程中，主要依靠在訓練之中獲得的權重，這將直接影響數據的處理與最后的結果。在一般的神經網絡進行實驗中，采用的是小樣本的方法，這使得整個模型在訓練學習的過程簡化了，也使得模型不能夠得到足夠多的數據來支持他的結論。神經網絡又稱為人工智能，主要是因為他可以在人為給定的數據中，自主的學習，尋找給定的數據之間的聯系與關系，從而進行最后給定的數據的分類，如果人為給定的數據量很少，則整個網絡無法得到有效的訓練和學習，從而在最后判定數據的分類上存在一定的偏向性。
　　2.1地表水環境質量評價標準
　　實驗的標準采用2002年6月1日實施的水質評價標準GB3838-2002的評價標準，采用了在標準中的DO、BOD5、石油類、揮發酚、氨氮、高錳酸鉀指數，這6項指標作為評價項目。具體標準見表1。
　　表1地表水環境質量標準（GB3838-2002）單位（mg/L）
　　               　　
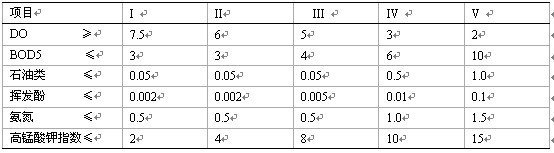
　　2.2檢測樣本
　　在實驗的數據上，本實驗選取參考文獻[2]中的水質監測資料作為檢驗數據，見表2。
　　表2檢驗數據單位（mg/L）

                 
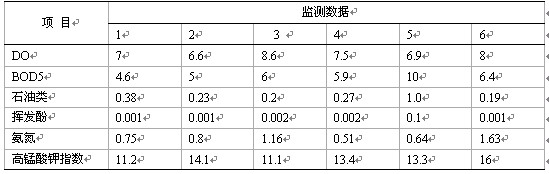
　　　　2.3訓練樣本
　　采用小樣本直接使用水質標準，其在二維平面內的投影分布見圖1。
　　大樣本采用MATLAB提供的RAND函數在各級評價標準內按隨機均勻分布方式線形插生成訓練樣本，每級生成200個樣本，共生成1000個訓練樣本。對應的目標輸出理論值I級為1，II級為2，其他依此類推。其在二維平面內的投影分布見圖2
　　對于BP-LM網絡模型，其評價結果屬于I級水質的輸入，期望輸出應為０～１之間的數值；對于評價結果屬于II級水質的輸入，期望輸出應為1～2之間的數值；其他依此類推。
　　對于LVQ網絡模型，其評價結果屬于I級水質的輸入，期望輸出應為１；對于評價結果屬于II級水質的輸入，期望輸出應為2；其他依此類推。
　　            
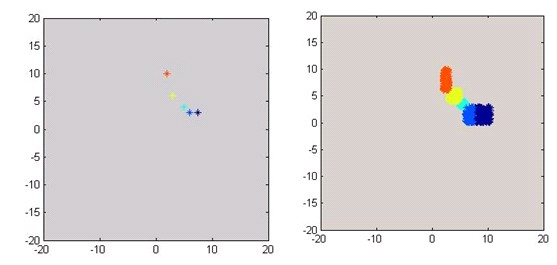
　　                                        圖1小訓練樣本在空間中的分布                                 圖2大訓練樣本在空間中的分布
　　3BP-LM網絡模型的建立及仿真結果
　　3.1BP-LM神經網絡的原理與結構
　　3.1.1原理
　　BP網絡，即多層前饋神經網絡，因其采用誤差反向誤差傳播算法(ErrorBackpropagation)而得名，1986年由D.E.Rumelhart等人提出。BP算法結構簡單、易于實現。BP網絡是一種分層型網絡，由輸入層、隱含層、輸出層組成。層與層之間采用全互連方式，同一層的單元則相互不連接，輸入層和輸出層的單元數是由具體問題的輸入層參數和輸出層參數來確定的，而隱含層的單元數則由具體問題的復雜程度、誤差下降情況等來確定。基本運行機制是：由信息正向傳播和誤差反向傳播2個過程組成，工作原理詳見文獻[3-6]。
　　
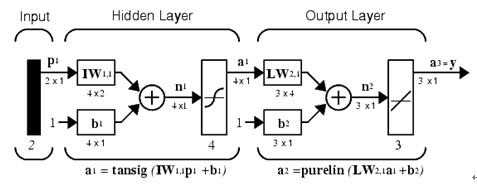
　　                                                            圖3BP網絡的結構
　　圖3中所示的BP網絡模型，輸入為2維向量；1個隱含層，4個隱含神經元，傳遞函數為tansig；輸出層3個神經元的結構，傳遞函數為purelin。
　　把輸入模式映射到相應分類器所需知識由權值來體現。最初，被給定問題域的權值是未知的，直到找到有用權值之前，神經網絡不能解決這個問題。尋找有用權值集合的過程，稱為訓練。在介紹網絡模型的訓練之前，引入一個概念：目標網絡誤差，即度量網絡收斂到其期望值的程度的度量值。
　　訓練步驟可歸納如下：
　　（1） 初始化，選定結構合理的網絡，置所有可調參數(權重和偏量)為均勻分布的較小數值；
　　（2） 對每個輸入樣本作前向計算；
　　（3） 當數據處理達到目標網絡誤差時，訓練完畢，反之則進行反向計算，即將輸入樣本再次輸入和在前一次計算中得到修正的權重一起訓練，再次修正權重。
　　這樣，整個網絡經過訓練和學習而具有鑒別能力，在給定一個表示輸入模式的由一系列特征組成的輸入向量后，訓練過的網絡就可以作為強識別器來使用。
　　相對于其他的網絡模型來比較，BP網絡要成熟的多，但他的問題也相對比較突出，比如收斂速度慢以及存在所謂局部最小值的問題。這些可以通過Levenberg-Marquardt（簡稱LM）算法來解決。
　　設X(k)表示第k次迭代的權值和偏量所組成的向量，新的權值和偏量組成的向量XK+1可根據下面的規則求得：
　　XK+1＝X(K)十△X(1)
　　對于牛頓法則是：
　　△X＝-[▽2E(x)]-1-▽E(x)(2)
　　(2)式中▽2E(x)表示誤差指標函數E(x)的Hessian矩陣；▽E(x)表示梯度。
　　設誤差指標函數為：
　　E（X）=1/2ΣNi=1ei2(x)(3)
　　(3)式中e(x)為誤差，那么：
　　▽E(x)=JT(x)e(x)（4）
　　▽2E(x)=JT(x)e(x)+S(x)（5）
　　在（4）、（5）式中S(x)=ΣNi=1ei(x)▽2ei(x)為Jacobian矩陣。
　　對于高斯-牛頓法的計算法則有：
　　△X＝-[JT(x)JT(x)]-1JT(x)e(x)(6)
　　LM算法是一種改進的高斯-牛頓法，它的形式為：
　　△X＝-[JT(x)JT(x)+μI]-1JT(x)e(x)(7)
　　從（7）式可看出，如果比例系數μ=0。則為高斯-牛頓法；如果μ取值很大，則LM算法接近梯度下降法。每迭代成功一步，則μ減小一些，這樣在接近誤差目標的時候，逐漸與高斯-牛頓法相似。高斯-牛頓法在接近誤差的最小值的時候，計算速度更快，精度也更高。由于LM算法利用了近似的二階導數信息，它比梯度下降法快得多，實踐證明，采用LM算法可以較原來的梯度下降法提高速度幾十甚至上百倍。另外由于[JT(x)J(x)+μI]是正定的，所以(7)式的解總是存在的。從這個意義上說，LM算法也優于高斯-牛頓法，因為對于高斯-牛頓法來說，JTJ是否滿秩還是個潛在的問題。在實際的操作中，μ是一個試探性的參數，對于給定的μ，如果求得的△x能使誤差指標函數量E(x)降低，則μ降低；反之，則μ增加[7]。
　　3.1.2網絡模型結構
　　網絡輸入為6維向量；采用一個隱含層，13個神經元，傳遞函數為tansig；輸出層1個神經元，傳遞函數采用purelin。
　　網絡訓練函數為tainlm（MATLAB中實現LM訓練算法的函數）；網絡性能函數為MSE，其目標值為1e-5；總迭代周期Epochs=1000；將MATLAB隨機數字產生器初始狀態置為0（固定這個變動因素）。
　　在隱含層神經元的選擇上，理論證明，如果一個隱含層有足夠多的節點，就可以達到所需的識別精度。在水質評價問題上，建議采用一個隱含層。隱含層神經元數的選取尚無理論上的指導，一般是根據經驗選取。對單隱含層BP網絡，常用的估算方法有[8,9]：
　　N=MNz/(Nx+Nz)或N2≥NxNz或N=log2M或N2=MNz
　　式中，N為隱含層神經元數；M為學習樣本容量；Nx、Nz分別為輸入、輸出層節點數。當學習樣本容量不大時，由上式確定的N往往偏小，難以進行非線性識別。因此，Ny應選得稍大一些。N值究競選取多大合適?經驗方法是試算，即從較多的隱含層開始，然后加以適當舍棄；或從較少的隱含層節點出發，逐漸加多。在本實驗中，根據以上原則，先按上式估算，然后選取大于N的一系列值，在模型中進行測試。結果顯示，當神經元個數取13時，效果最好。
　　3.2BP-LM網絡小樣本訓練及結果
　　3.2.1訓練過程
　　網絡經過7個迭代周期的訓練，性能函數下降到8.2653e-6，小于其目標1e-5，訓練結束。訓練過程如圖4所示。
　　             
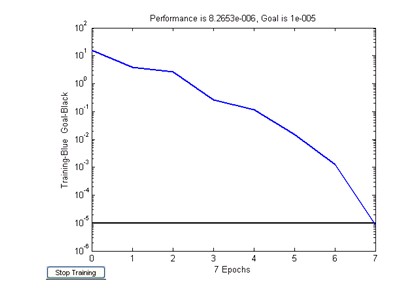
　　圖4BP-LM網絡小樣本訓練過程中網絡性能下降曲線
　　3.2.2網絡模型的仿真結果
　　將水質評價標準的各項污染指標分界值（表1）輸入已訓練好的網絡模型，對應的網絡模型輸出值分別為0.9999、2.0000、3.0000、4.0000、4.9999。顯然，對應于I-V類水質，該網絡模型輸出值的范圍分別為：(0，0.9999]、(0.9999，2.0000]、(2.0000，3.0000]、(3.0000，4.9999]和＞4.9999。
　　表3小樣本訓練的模型對檢測樣本的評價結果

                            
　　將檢測樣本輸入網絡模型，得到的輸出分別為3.2999、3.3591、3.4745、3.1613、3.2450、3.9969，均對應為4類水質，這與模糊綜合評判法分類結果一致[10]（見表3）。
　　3.3BP-LM網絡大樣本訓練及結果
　　3.3.1訓練過程
　　網絡經過68個迭代周期的訓練，性能函數下降到6.60625e-6，小于其目標1e-5，訓練結束。訓練過程如圖5所示。
　　                     
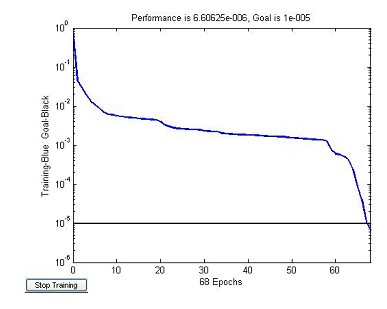
　　                                        圖5BP-LM網絡大樣本訓練過程中網絡性能下降曲線
　　3.3.2網絡模型的仿真結果
　　將水質評價標準的各項污染指標分界值（表1）輸入已訓練好的網絡模型，對應的網絡模型輸出值分別為1.9819、2.3773、3.0298、4.5679、5.0000。這樣，對應于I-V類水質，其網絡模型輸出值的范圍分別為：(0，1.9819]、(1.9819，2.3773]、(2.3773，3.0298]、(3.0298，5.0000]和＞5.0000。
　　將檢測樣本輸入網絡模型，得到的輸出分別為3.0413、3.9996、2.9994、3.9669、3.9827、3.9996；即第1，2，4，5，6項檢測樣本屬于IV類，第3項屬于III類。這與模糊綜合評判法分類結果稍有差別（見表4）。
　　表4大樣本訓練的模型對檢測樣本的評價結果

                      
　　4.LVQ網絡
　　4.1LVQ網絡的原理方法與網絡模型結構
　　4.1.1LVQ網絡的原理與方法
　　LVQ網絡，即學習向量化網絡(LearnVectorQuantization).網絡的結構示意圖見圖6。
　　LVQ網絡有兩層組成，第一層為競爭層，第二層為線性層。競爭層能夠學習對輸入向量的分類，這與自組織競爭網絡非常相似。線性層將競爭層傳來的分類信息轉變成為使用者所定義的類別。可以將競爭層學習得到的類稱為子類，將線性層習得到的類稱為目標類。
　　LVQ算法是對SOM（Self-OrganizingMaps，自組織映射）算法的一種擴展，它的基本思想源于SOM算法，它對應的網絡結構與SOM很相似，但并不像SOM網絡那樣存在某種特定的拓撲結構。LVQ算法是一種監督型的聚類方法，該算法與SOM算法最大的區別在于提供給LVQ網絡的每個訓練例都有一個“標記”(1abel)，該“標記”用于指明每個訓練例所屬的類別，在網絡的訓練過程中起到一定的監督作用。因此，LVQ算法實際上是SOM算法基本思想在監督學習領域中的一種應用，是Kohonen的有監督學習的擴展形式。融合了自組織和有導師監督的技術，學習方法是競爭的，但產生方式是有教師監督的，也就是說，競爭學習是在由訓練輸入指定的各類中局部進行。
　　                
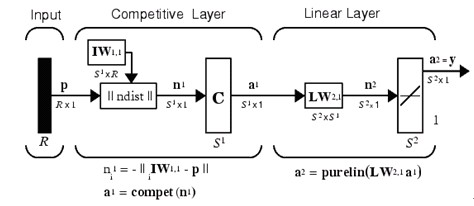
　　                                                               圖6LVQ網絡結構
　　LVQ算法可在監督狀態下對競爭層進行訓練，在競爭層中網絡將根據給定的輸入、輸出特征自動學習適應樣本特性并對輸入樣本分類，其具體的工作步驟為：
　　（1）每輸出一個樣本X后，在輸出陣列中找出具有最大的單元C；
　　（2）設X所屬類別以知為Ｒ，而在第一階段學習中Ｃ的類別為Ｓ，則權值按如下公式調整：
　　wc(t+1)=wc(t)+u(t)[x(t)-wc(t)]r=s
　　wc(t+1)=wc(t)-u(t)[x(t)-wc(t)]r≠s
　　wi(t+1)=wir≠s
　　由上式可見，若對x分類真確，則使Ｃ的權更靠近Ｘ，否則則遠離。對不是最大輸出的單元，權值不動。
　　LVQ網絡的訓練過程如下：
　　（1） 初始化權向量，設置初始學習率；
　　（2） 從訓練集中選取一輸入向量X，找出與X具有最小Euclidean距離的權向量WK；
　　（3） 調整神經元k的權向量；
　　（4） 訓練集中選取另外一個輸入向量提供給LVQ網絡，返回步驟2)直到所有的向量都提供了一遍為止。
　　（5） 減小學習率α，并且測試停止條件是否滿足，如果滿足則停止訓練，否則返回步驟2)。
　　詳細的LVQ網絡的訓練算法參見參考文獻[11-12]。
　　4.1.2LVQ網絡模型的結構
　　網絡輸入為6維向量；競爭層采用15個神經元；輸出層為要求輸出數據格式為向量模式，在MATLAB中采用轉換函數（ind2vec）將分類類別數據轉換為向量模式；網絡性能函數為MSE，其目標值為1e-5；總迭代周期Epochs=1000；將MATLAB隨機數字產生器初始狀態置為0（固定這個變動因素）；競爭層神經元數也是在不斷在摸索的基礎上比較優缺點，最后確定是15個為最佳。
　　4.2LVQ網絡小樣本訓練與結果
　　4.2.1網絡模型的訓練
　　網絡經過553個迭代周期的訓練，性能函數下降至小于其目標1e-5，訓練完成。訓練過程如圖7所示。
　　4.2.2網絡模型的仿真結果
　　將水質評價標準的各項污染指標分界值（表1）輸入已訓練好的網絡模型，對應的網絡模型輸出結果用轉換函數vec2ind轉換為標量，理論結果應為1、2、3、4、5，分別對應于I到V類水質，實際輸出結果與此完全一致。將檢測樣本輸入網絡模型，同樣對輸出結果采用轉換函數vec2ind轉換為標量，結果分別為3、3、3、3、3、5，即前五項檢測樣本的評價結果為III類水質，第六項檢測樣本的評價結果為V類水質。這與模糊綜合評判結果均不同。
　　        
　　
　                                     　圖7LVQ網絡小樣本訓練過程圖
　　4.3LVQ網絡大樣本訓練的實驗
　　4.3.1網絡模型的訓練
　　網絡訓練到16個迭代周期后，性能函數始終在0.004附近振蕩，直到完成1000次迭代周期，即訓練結束時也未下降至小于其目標1e-5。訓練過程如圖8所示。
　　              
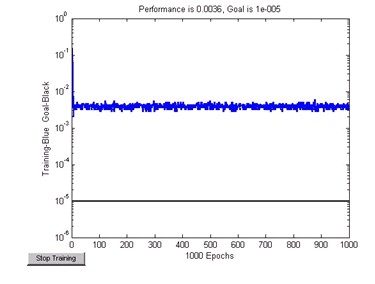
　　                                                 圖8LVQ網絡大樣本訓練過程圖
　　4.3.2網絡模型的仿真結果
　　將水質評價標準的各項污染指標分界值（表1）輸入已訓練好的網絡模型，對應的網絡模型輸出結果用轉換函數vec2ind轉換為標量，理論結果應為1、2、3、4、5，分別對應于I到V類水質，實際輸出結果為2、3、3、4、5。顯然，該網絡模型沒有得到有效的訓練，其性能不能滿足水質評價的要求。
　　5分析與討論
　　5.1BP-LM網絡模型的分析
　　對于BP-LM網絡模型，采用小訓練樣本訓練，網絡只用了7次迭代周期就完成了訓練，收斂很快。網絡模型對檢驗樣本的輸出值與預定目標接近，也與模糊綜合評判法一致。
　　采用大訓練樣本訓練，由于網絡運算量顯著增加，網絡經過了68次迭代周期才完成訓練，收斂速度相對于小樣本訓練要慢一些。網絡模型對的第3項檢測樣本的評價結果與模糊綜合評判法有出入，網絡模型評價為III類水質，而模糊綜合評判法評價為IV類水質。
　　關于神經網絡模型對檢測樣本的評價結果與模糊綜合評判法評價結果的一致性與否，并不能作為神經網絡模型合理性或準確性的評價依據。因為模糊綜合評判法的結果受人為因素的影響很大，具有主觀性和不確定性，而神經網絡模型基本不受人為因素影響，而且神經網絡模型是通過對訓練樣本的學習，將分類的潛在規律或規則儲存于網絡的連接權重中。從這一點上來說，神經網絡模型比模糊綜合評判法更符合水質評價的原理。
　　本試驗中，小樣本訓練的模型對檢測樣本給出的評價結果與模糊綜合評判法完全一致，而大樣本訓練的模型對第3項檢測樣本的評價結果與后者評價結果不一致。本文認為不能據此判斷小樣本訓練得到的模型要優于大樣訓練得到的模型。BP神經網絡的訓練，理論上需要大量的有代表性的樣本，這樣得到的模型才比較可靠。很顯然，小樣本不是代表性的訓練樣本，而大樣本則體現了對所有輸入樣本的代表性。
　　在整個BP-LM網絡模型仿真過程中，BP-LM網絡的優點體現的很明顯：
　　（1） BP-LM網絡不必人為地考慮因子之間的權值、閾值。它能通過樣本實際輸出與期望輸出的誤差比較和修改學習參數,自動地進行調整和適應[13]；
　　（2） BP-LM網絡建模簡單、計算量少、速度快；
　　（3） BP-LM網絡具有一定的泛化能力；
　　（4） 網絡能通過學習帶正確答案的實例集自動提取“合理的”求解規則，即具有自學習能力；
　　（5） BP-LM網絡實質上實現了一個從輸入到輸出的映射功能，而數學理論已證明它具有實現任何復雜非線性映射的功能。這使得它特別適合于求解內部機制復雜的問題[14]。
　　5.2LVQ網絡模型的分析
　　在本次實驗中，LVQ并沒有很好的完成期望目標，在小樣本訓練的實驗中，盡管運算量小，但是由于LVQ算法較BP算法復雜，網絡收斂速度慢，訓練經過553次迭代周期才結束。而大樣本訓練更增加了LVQ網絡的運算量，網絡訓練速度非常慢，在CPU為IntelP41.7GHz、內存為256MB的計算機上，經過2個小時才完成1000次的迭代周期，但網絡的性能函數下降不明顯，遠未達到預期性能目標。
　　理論上，LVQ網絡模型非常適合解決模式識別問題。但本次試驗中發現LVQ網絡訓練的收斂速度以及對水質評價問題的處理結果都很不理想。一方面說明LVQ網絡不適宜于用大樣本來訓練；另一方面，LVQ網絡的訓練樣本要求更嚴格的代表性。
　　5.3BP-LM網絡與LVQ網絡的對比分析
　　在BP-LM網絡實驗中，很好的表現出BP-LM網絡的優點，簡潔、建模簡單、計算量少、速度快、很強的自我學習能力。LVQ網絡由于迭代過多，運算繁瑣，需要占用了大量的內存空間，LVQ網絡在目前還不適宜做水質評價工作，尤其是需要有大量樣本來訓練的水質評價工作。相比之下，BP-LM網絡模型更適合于水質評價工作，特別是訓練樣本容量很大的情況下。
　　5.4訓練樣本的代表性問題
　　水質評價的神經網絡模型需要構建具有代表性的訓練樣本進行訓練。直接采用水質評價標準的分界指標值作為訓練樣本，本文認為這樣的訓練樣本不具有代表性；同時，樣本容量也過少。本文采用隨機方法插值生成的、均勻分布的大樣本，解決了訓練樣本的代表性和容量的要求，但樣本的均勻分布沒有考慮到水質評價標準分級的模糊性。如果采用正態分布的大訓練樣本，可能會解決這個問題，并有可能加快神經網絡訓練的收斂速度。這有待于進一步的試驗來驗證。
　　
　　參考文獻
　　[1]鄭建青.2003.水環境質量評價的灰色局勢決策法.科技與管理,3:29-31.
　　[2]樓文高、王廷政.2003.基于BP網絡的水質綜合評價模型及其應用.環境污染治理技術與設備,8(4):23-26.
　　[3]陳古余.上海市海岸帶和海涂資源綜合調查報告.上海:上海科學技術出版社，1988.
　　[4]顧德宇，湯容坤.1995.大亞灣沉積物間隙水的無機磷硅氮營養鹽化學.海洋學報，17(5):73-80.
　　[5]韓舞鷹，容榮貴，黃西能等.1986.海水化學要素調查手冊.北京:海洋出版社，，103-113,121-148.
　　[6]金相燦，層清英主編.1990.湖泊富營養化調查規范.第2版.北京:中國環境科學出版社,208-238.
　　[7]阮體年、黨競良、胡曉寒等.2004.基于LM-BP算法的綜合水質評價研究.水資源研究,25(1):12-14.
　　[8]馬細霞、賀曉菊、趙道全.2002.BP網絡隱含層對水質評價結果的影響分析.水電能源科學,20:(3)16-18.
　　[9]韓力群.2001.人工神經網絡理論、設計及應用.北京:化學工業出版社,123-125.
　　[10]樓文高、王廷政.2003.基于BP網絡的水質綜合評價模型及其應用.環境污染治理技術與設備,8(4):23-26.
　　[11]張敏靈、陳兆乾、周志華.2002.SOM算法、LVQ算法及其變體綜述.計算機科學,29(7):97-100..
　　[12]FranciscoS.etal.2002.AssessmentofGroundwaterQualitybyMeansofSelf-OrganizingMaps:ApplicationinaSemiaridArea.EnvironmentalManagement,30(5):716–726.
　　[13]徐婷婷、姜林、彭荔紅.B-P網絡應用于地下水水質監測點優選.中國環境監測.
　　[14]劉遂慶、王延政、樓文高.2003.基于概率論和BP網絡的水質評價與灰色動態預測模型.上海環境科學,22(10):673-681.
　　ComparisonStudiesonNeuralNetworkModels
　　forWaterQualityEvalutation
　　
　　Abstract:ThispaperpresentedtwoneuralnetworkmodelsforsurfacewaterqualityevaluationconstructedwithMATLAB7.TheresultsshowedthatthecalculatingvelocityandconvergingvelocityofBP-LMmodelwasfarfasterthanLVQmodel,andBP-LMmodelissuitedtoevaluatewaterquality.Influencesoftrainingsamplesizeontwoneuralnetworkmodelswereobserved.ItisfoundthatLVQmodelwassensitivetotrainingsamplesize,butBP-LMmodeldidn’tso.TherootcauseisthatcalculatingprocessofLVQalgorithmismorecomplicatedthanthatofBP-LMalgorithm.
　　Keywords:artificialneuralnetwork;BP-LM;LVQ;trainingsample;waterqualityevaluation